10/4/2021
Por Alfonso Merla

"Compensación De Potencia Reactiva En Sistemas Eléctricos"

Que tal Ingeniero bienvenido a este artículo que tenemos para ti, de este tema relevante e importante en los sistemas eléctricos que es el factor de potencia y como influye la potencia reactiva en los sistemas eléctricos, así que saca tu cuaderno y pluma que este articulo esta que arde. 👷🔥

Bancos de capacitores de media tensión

Este artículo arrojará algo de luz sobre cómo la adición de banco de capacitores le da al sistema de distribución la potencia reactiva necesaria para devolver el factor de potencia al nivel requerido. Los capacitores actúan como una fuente de energía reactiva, lo que en consecuencia reduce la potencia reactiva que debe suministrar la fuente de energía. Por tanto, se mejora el factor de potencia del sistema.

En una instalación que consume potencia reactiva Q1 (diagrama 1), la adición de un banco de capacitores que genera una potencia de compensación reactiva Qc (diagrama 2) mejora la eficiencia general de la instalación. La potencia reactiva Q1 inicialmente suministrada por la fuente se reduce a un nuevo valor Q2 (diagrama 3), el ángulo φ es menor y el coseno de este ángulo se mejora (se mueve hacia 1).

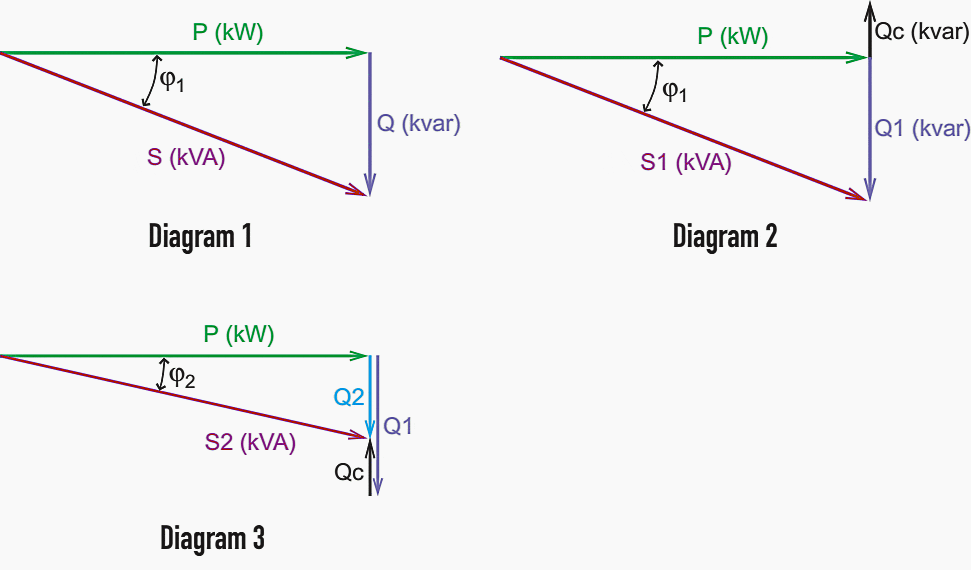
Diagrama 1,2 y 3 de los ejemplos aquí arriba descritos del triángulo de potencia

La compensación de potencia permite conjugar los intereses del usuario y los de la empresa distribuidora de energía, mejorando la eficiencia de las instalaciones mediante un mejor aprovechamiento de la potencia disponible limitando el consumo de energía reactiva que no solo es innecesaria y costosa sino también una fuente de sobrecorrientes en conductores.

El siguiente ejemplo muestra cómo, al “incrementar” el factor de potencia de 0,7 a 0,95, para la misma potencia activa de 100 kW, la potencia aparente S (VA), en comparación con la que realmente debe ser suministrada, se ha reducido en 35%.

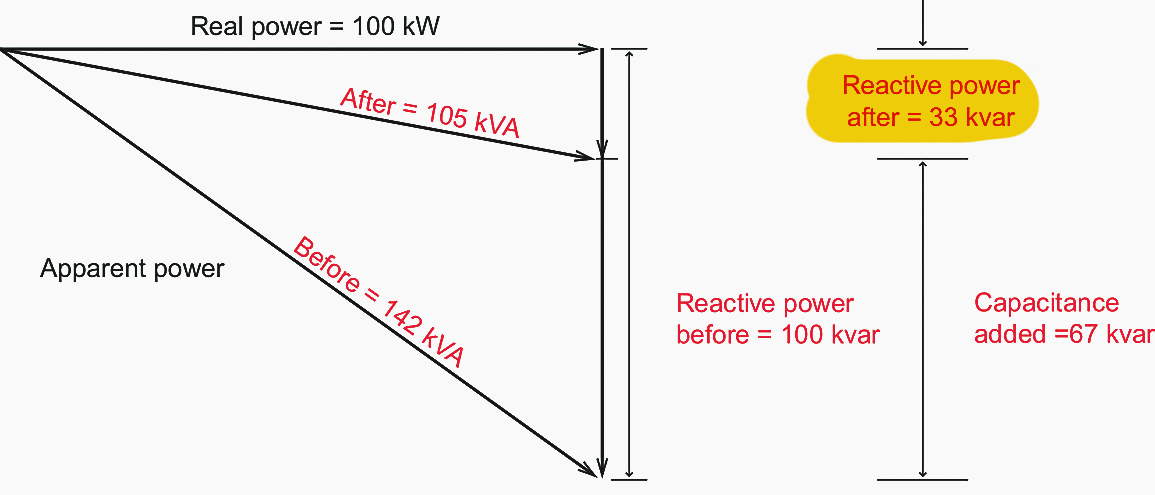
Ejemplo de aumento de factor de potencia

Cálculos del factor de potencia:

  • Antes de PF = 100/142 = 0,70 o 70%
  • Después de PF = 100/105 = 0,95 o 95%

Cuando el cos cambia de un valor inicial cos φ1 a un valor final cos φ 2 , como regla general, las pérdidas óhmicas se reducen en: (1 - (cos φ1 / cos φ2) ²) × 100 como%

Por tanto, el cambio de un cosφ de 0,7 a 0,95 reduce las pérdidas en un 45%. Por tanto, un cosφ bajo provoca caídas de tensión en los conductores. La caída de voltaje en una línea eléctrica se puede calcular usando la fórmula: ΔU = I (R cosφ + L sinφ). La potencia máxima que se puede transmitir en un sistema de CA se calcula utilizando las siguientes fórmulas:

P = UI cosφ para monofásico y P = UI √3 cosφ para trifásico.

Para la misma corriente, la potencia transmitida es directamente proporcional al cos φ. Por lo tanto, cambiar de un cos φ de 0,7 a 0,95 permite aumentar la potencia activa (en W) en un 35% y reducir las pérdidas de calor de línea asociadas y las caídas de tensión (ver arriba). La potencia que puede entregar un transformador se expresa en kVA. Este es el poder aparente disponible. Se hará un mejor uso de este transformador si el cos φ de la carga es cercano a 1.
 

Al mejorar el cos φ de un valor inicial cos φ1 a un valor final cos φ 2 , para X (W) potencia utilizada, se libera una potencia aparente utilizable adicional de S (kVa) = p (kW) × ((1 / cos φ1) - (1 / cos φ 2 )). Por lo tanto, un transformador de 1000 kVa que entrega una carga de 700 kW con un cosφ de 0,7 está en su carga máxima.